Олимпиадная задача по планиметрии о треугольнике с медианами, 8–9 класс
Задача
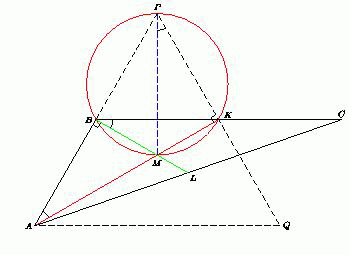
В неравнобедренном треугольнике ABC проведены медианы AK и BL . Углы BAK и CBL равны30o . Найдите углы треугольника ABC .
Решение
Пусть прямая AB пересекается с прямой, проходящей через точку K перпендикулярно медиане AK , в точке P . На продолжении отрезка PK за точку K отложим отрезок KQ = PK . Из прямоугольного
треугольника APK находим, что  APK = 60o . В треугольнике APQ высота AK является медианой, значит, этот треугольник –
равнобедренный, а т.к. один из его углов равен60o , то
треугольник APQ – равносторонний.
APK = 60o . В треугольнике APQ высота AK является медианой, значит, этот треугольник –
равнобедренный, а т.к. один из его углов равен60o , то
треугольник APQ – равносторонний.
Пусть M – точка пересечения медиан треугольника ABC . Тогда 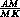 =
= 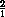 . Таким образом, точка M , лежащая на
медиане треугольника APQ , делит её в отношении 2:1, считая от вершины.
Значит, M – точка пересечения медиан треугольника APQ , т.е.центр
этого правильного треугольника.
. Таким образом, точка M , лежащая на
медиане треугольника APQ , делит её в отношении 2:1, считая от вершины.
Значит, M – точка пересечения медиан треугольника APQ , т.е.центр
этого правильного треугольника.
Тогда  KPM = 30o =
KPM = 30o =  KBM , поэтому точки M , K , P и B лежат на одной окружности, причём PM – диаметр этой окружности,
т.к.
KBM , поэтому точки M , K , P и B лежат на одной окружности, причём PM – диаметр этой окружности,
т.к.  PKM = 90o . Но тогда и
PKM = 90o . Но тогда и  PBM = 90o . Следовательно,
PBM = 90o . Следовательно,
 ABC =
ABC =  ABM +
ABM +  MBK = 90o+30o = 120o.
MBK = 90o+30o = 120o.
Пусть сторона треугольника APQ равна2a . Тогда
AB = 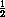 AP = a, BK= a, BC = 2BK = 2a.
AP = a, BK= a, BC = 2BK = 2a.
AC = 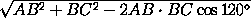 =
=
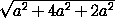 = a
= a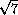 .
.
cos  ACB =
ACB = 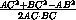 =
= 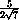 ,
,
cos  CAB =
CAB = 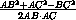 =
= 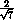 .
.
Ответ
 ABC = 120o ,
ABC = 120o ,  BAC = arccos
BAC = arccos 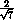 ,
,  ACB = arccos
ACB = arccos 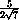 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь