Олимпиадная задача по планиметрии для 8–9 класса: доказательство окружности через четыре точки
Задача
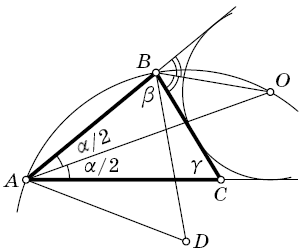
Окружность с центром D проходит через вершины A, B и центр O вневписанной окружности треугольника ABC , касающейся его стороны BC и продолжений сторон AB и AC. Докажите, что точки A, B, C и D лежат на одной окружности.
Решение
Обозначим углы треугольника ABC через α, β и γ соответственно. Поскольку BO – биссектриса внешнего угла при вершине B треугольника ABC, а AO – биссектриса угла BAC, то ∠AOB = 180° – ∠BAO – ∠ABO = 180° – α/2 – (β + ½ (α + γ)) = γ – γ/2 = γ/2. Поскольку ADB – центральный угол окружности, проходящей через точки A, B и O, а AOB – угол, вписанный в эту окружность, то ∠ADB = 2∠AOB = γ = ∠ACB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет