Олимпиадная задача по планиметрии для 8-9 класса: перпендикулярность B'I и KL в треугольнике
Задача
Пусть B' — точка описанной окружности остроугольного треугольника ABC , диаметрально противоположная вершине B ; I — центр вписанной окружности треугольника ABC ; M — точка касания вписанной окружности со стороной AC . На сторонах AB и BC выбраны соответственно точки K и L , причём KB=MC и LB=AM . Докажите, что прямые B'I и KL перпендикулярны.
Решение
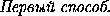 Достаточно доказать, что B'K2-B'L2=IK2-IL2.
Пусть радиус описанной окружности треугольника ABC равен R ,
полупериметр треугольника равен p , а вписанная окружность радиуса r касается сторон AB и BC в точках X и Y соответственно. Обозначим AB=c , AC=b , BC=a . Тогда
Достаточно доказать, что B'K2-B'L2=IK2-IL2.
Пусть радиус описанной окружности треугольника ABC равен R ,
полупериметр треугольника равен p , а вписанная окружность радиуса r касается сторон AB и BC в точках X и Y соответственно. Обозначим AB=c , AC=b , BC=a . Тогда
BK=CM = p-AB=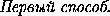 -c=
-c= ,
,
BL=AM=p-BC=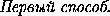 -a=
-a= ,
,
BX=BY=p-AC=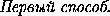 -b=
-b=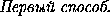 ,
,
AK=AB-BK=c- =
=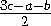 ,
,
CL=BC-BL=a- =
=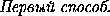 ,
,
XK=|BX-BK|=|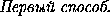 -
- |=
|c-b|,
|=
|c-b|,
LY=|BY-BL|=|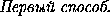 -
- |=
|a-b|.
|=
|a-b|.
Из прямоугольных треугольников ABB' , CBB' , KPI и LQI находим, что
AB'2=BB'2-AB2=4R2-c2, CB'2=BB'2-CB2=4R2-a2,
B'K2=AK2+AB'2=(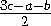 )2+4R2-c2,
)2+4R2-c2,
B'L2=CL2+CB'2=(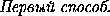 )2+4R2-a2,
)2+4R2-a2,
IK2=XK2+IX2=(c-b)2+r2, IL2=LY2+IY2=(a-b)2+r2,
B'K2-B'L2=(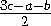 )2+4R2-c2-
(
)2+4R2-c2-
(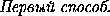 )2-4R2+a2=
)2-4R2+a2=
=(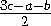 )2-(
)2-(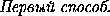 )2+
a2-c2=(a-c)(2b-a-c),
)2+
a2-c2=(a-c)(2b-a-c),
IK2-IL2=(c-b)2+r2- (a-b)2-r2=(a-c)(2b-a-c)=B'K2-B'L2.
 Отложим от точки B вектор
Отложим от точки B вектор 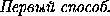 , равный вектору
, равный вектору 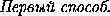 . Достаточно доказать, что BT
. Достаточно доказать, что BT 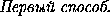 KL .
Поскольку BB' — диаметр окружности, то
KL .
Поскольку BB' — диаметр окружности, то
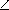 BAB' =
BAB' = 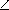 BCB'= 90o,
BCB'= 90o,
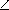 ABT =
ABT = 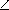 CBT' = α.
CBT' = α.
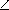 ABC -α), проекции отрезка BT' на эти же стороны равны соответственно BT' cos (
ABC -α), проекции отрезка BT' на эти же стороны равны соответственно BT' cos ( ABC -α)и BT' cos α . Значит, проекции вектора
ABC -α)и BT' cos α . Значит, проекции вектора  на
стороны AB и BC равны проекциям вектора
на
стороны AB и BC равны проекциям вектора  на
стороны BC и AB соответственно, а т.к. AX=AM=BL и CY=CM=BK ,
то проекции вектора
на
стороны BC и AB соответственно, а т.к. AX=AM=BL и CY=CM=BK ,
то проекции вектора  на стороны BC и AD равны
соответственно
на стороны BC и AD равны
соответственно 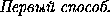 и
и 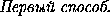 . Поэтому
. Поэтому
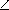 BKT' =
BKT' = 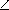 BLT' = 90o,
BLT' = 90o,
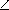 BT'K =
BT'K = 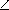 BLK,
BLK,
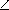 TBL +
TBL + 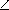 BLK =
BLK = 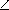 T'BK +
T'BK + 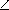 BT'K= 90o.
BT'K= 90o.
 KL .
KL .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь