Олимпиадная задача по планиметрии для 8–9 классов: доказательство в параллелограмме

  Первый способ. Пусть при параллельном переносе на вектор 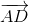    точка O перешла в точку E (рис. слева). Тогда AOED – параллелограмм, поэтому  ∠OED = ∠OAD = ∠OCD.

  Значит, точки C, E, O и D лежат на одной окружности. Вписанные углы ODC и OEC равны, а так как BOEC – параллелограмм, то  ∠OEC = ∠OBC.  Следовательно,  ∠OBC = ∠ODC.

  Второй способ. Пусть прямая, проведённая через точку O параллельно сторонам AD и BC, пересекает стороны AB и CD соответственно в точках K и M (рис. справа), а прямая, проведённая через точку O параллельно сторонам AB и CD, пересекает стороны BC и AD соответственно в точках L и N. Тогда  ∠CMO = ∠CDA = ∠ONA,  значит, треугольники OAN и OCM подобны по двум углам. Поэтому  AN : CM = ON : OM.  Поскольку  ∠OLB = ∠OND  и при этом  BL : LO = AN : CM = ON : OM = DM : OM,  то треугольники OBL и ODM подобны по двум сторонам и углу между ними. Следовательно,

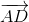
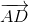
∠LBO = ∠ODM, что и требовалось.

Ответ задачи отсутствует