Олимпиадная задача по планиметрии для 8-9 класса: площади криволинейных треугольников (автор Толпыго А. К.)
Задача
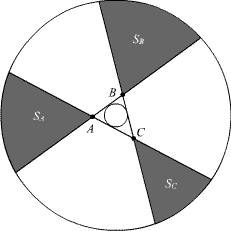
Учитель продиктовал классу задание, которое каждый ученик выполнил в своей тетради. Вот это задание: Нарисуйте две концентрические окружности радиусов 1 и 10. К малой окружности проведите три касательные так, чтобы их точки пересечения A, B и C лежали внутри большой окружности. Измерьте площадь S треугольника ABC и площади SA, SB и SC трёх образовавшихся криволинейных треугольников с вершинами в точках A, B и C. Найдите SA + SB + SC – S. Докажите, что у всех учеников (если они правильно выполнили задание) получились одинаковые результаты.
Решение
Рассмотрим хорды – отрезки касательных, заключённые внутри большой окружности. Сложив площади трёх отсекаемых этими хордами от большой окружности сегментов, не содержащих треугольника ABC, и вычтя площадь большого круга, мы получим как раз SA + SB + SC – S. Поскольку все три рассматриваемые хорды равноудалены от центра окружности, то площади упомянутых сегментов не зависят от положения касательных.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь