Назад

Олимпиадная задача по планиметрии: середины треугольника и одном точке (8-9 класс)

Задача 208604 • Сложность: 2 • 8-9 класс
Задача

На сторонах AB, BC и AC треугольника ABC взяты точки P, M и K так, что отрезки AM, BK и CP пересекаются в одной точке и 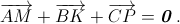     Докажите, что P, M и K – середины сторон треугольника ABC.

Решение

  Заметим (рис. слева), что

           
  Это значит, что из отрезков AK, CM и BP можно составить треугольник, подобный данному. Следовательно, стороны делятся в одном и том же отношении.

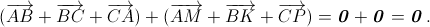
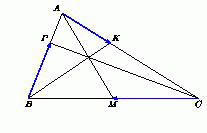
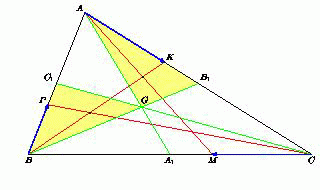
  Далее можно рассуждать по-разному.   Первый способ. По теореме Чевы (см. задачу 153856) это возможно, только когда это отношение равно 1.   Второй способ. Пусть 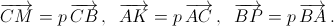    Обозначим через G точку пересечения медиан AA1, BB1 и CC1 треугольника ABC (рис. справа). Предположим, что  p < ½.  Тогда точка пересечения отрезков AM и BK лежит внутри треугольника AB1G, а точка пересечения отрезков CP и BK – внутри треугольника BC1G, что невозможно (эти точки совпадают по условию). Аналогично отвергается случай  p > ½.  Следовательно,  p = ½.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет