Олимпиадная задача по планиметрии: минимальное расстояние между прямой и окружностью (8–9 класс)
Задача
Точка M лежит на прямой 3x - 4y + 34 = 0, а точка N — на окружности x2 + y2 - 8x + 2y - 8 = 0. Найдите наименьшее расстояние между точками M и N.
Решение
Заметим, что
x2 + y2 - 8x + 2y - 8 = 0 $\displaystyle \Leftrightarrow$ x2 - 8x + 16 + y2 + 2y + 1 = 25 $\displaystyle \Leftrightarrow$ (x - 4)2 + (y + 1)2 = 52.
Значит, центр окружности — точкаQ(4; - 1), а радиус равен 5.
Пусть d — расстояние от точки Q до прямой
3x - 4y + 34 = 0. Тогда
d = $\displaystyle {\frac{\vert 3\cdot 4-4\cdot (-1) +34\vert}{\sqrt{3^{2}+4^{2}}}}$ = $\displaystyle {\textstyle\frac{50}{5}}$ = 10 > 5.
Значит, все точки данной прямой лежат вне данной окружности. Поэтому для каждой
точкиMданной прямой и каждой точкиNданной окружности
MN > MQ - QN = MQ - 5 > d - 5 = 10 - 5 = 5,
причём это расстояние равно 5, еслиM— проекция точкиQна данную прямую.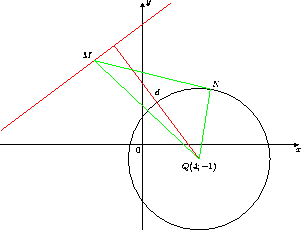
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет