Олимпиадная задача: уравнение окружности с центром в точке M(3;2), касательной к прямой
Задача
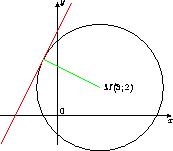
Составьте уравнение окружности с центром в точке M(3;2), касающейся прямой y = 2x + 6.
Решение
Первый способ.
Пусть радиус искомой окружности равен R. Тогда расстояние от точки M
до данной прямой также равно R. Запишем уравнение
этой прямой в общем виде (2x - y + 6 = 0) и воспользуемся формулой для расстояния
между точкой и прямой:
R = $\displaystyle {\frac{\vert 2\cdot 3-2 +6\vert}{\sqrt{2^{2}+1^{2}}}}$ = $\displaystyle {\frac{10}{\sqrt{5}}}$ = 2$\displaystyle \sqrt{5}$.
Следовательно, искомое уравнение имеет вид
(x - 3)2 + (y - 2)2 = 20.
Второй способ.
Искомое уравнение имеет вид
(x - 3)2 + (y - 2)2 = R2.
Подставим в левую часть этого уравненияy= 2x+ 6. После очевидных упрощений
получим квадратное уравнение5x2+ 10x+ 25 -R2= 0.
Поскольку прямая и окружность имеют единственную общую точку, то полученное
уравнение имеет ровно одно решение, значит, его дискриминант равен 0, т.е.
D = 100 - 20(25 - R2) = 20(5 - 25 + R2) = 20(R2 - 20) - 0.
Отсюда находим, чтоR2= 20. Следовательно, искомое уравнение имеет вид
(x - 3)2 + (y - 2)2 = 20.
Ответ
(x - 3)2 + (y - 2)2 = 20.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет