Олимпиадная задача: расстояние от точки до прямой — геометрические методы, 8-9 класс
Задача
Докажите, что расстояние от точки M(x0;y0) до прямой, заданной уравнением ax + by + c = 0, равно
$\displaystyle {\frac{\vert ax_{0}+ by_{0}+ c\vert}{\sqrt{a^{2}+ b^{2}}}}$.
Решение
Пусть данная прямая не параллельна координатным осям. Запишем её уравнение в виде y = - ${\frac{a}{b}}$x - ${\frac{c}{b}}$. Тогда её угловой коэффициент k1 = - ${\frac{a}{b}}$. Если k2 — угловой коэффициент прямой, перпендикулярной данной, то k1 . k2 = - 1. Поэтому
k2 = - $\displaystyle {\frac{1}{k_{1}}}$ = $\displaystyle {\frac{b}{a}}$.
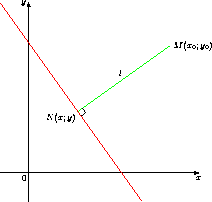
Уравнение прямойl, проходящей через точкуM(x0;y0) перпендикулярно данной прямой,
найдём по точке и угловому коэффициентуk2=${\frac{b}{a}}$:
y - y0 = $\displaystyle {\frac{b}{a}}$(x - x0).
Координаты точки N(x;y) пересечения данной прямой и прямой l удовлетворяют системе
уравнений
$\displaystyle \left\{\vphantom{ \begin{array}{lll}
y-y_{0}=\frac{b}{a}(x-x_{0})\\
ax + by + c = 0\\
\end{array} }\right.$$\displaystyle \begin{array}{lll}
y-y_{0}=\frac{b}{a}(x-x_{0})\\
ax + by + c = 0\\
\end{array}$ $\displaystyle \Leftrightarrow$ $\displaystyle \left\{\vphantom{ \begin{array}{lll}
y-y_{0}=\frac{b}{a}(x-x_{0})\\
a(x-x_{0}) + b(y-y_{0}) = -ax_{0}-by_{0}-c.\\
\end{array} }\right.$$\displaystyle \begin{array}{lll}
y-y_{0}=\frac{b}{a}(x-x_{0})\\
a(x-x_{0}) + b(y-y_{0}) = -ax_{0}-by_{0}-c.\\
\end{array}$
Отсюда находим, что
x - x0 = - $\displaystyle {\frac{b}{a^{2}+b^{2}}}$(ax0 + by0 + c), y - y0 = - $\displaystyle {\frac{a}{a^{2}+b^{2}}}$(ax0 + by0 + c).
Следовательно,
MN = $\displaystyle \sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}}$ =
= $\displaystyle \sqrt{\left(-\frac{b}{a^{2}+b^{2}}(ax_{0}+ by_{0}+ c)\right)^{2}+
\left(-\frac{a}{a^{2}+b^{2}}(ax_{0}+ by_{0}+ c)\right)^{2}}$ = $\displaystyle {\frac{\vert ax_{0}+ by_{0}+ c\vert}{\sqrt{a^{2}+ b^{2}}}}$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет