Олимпиадная задача по планиметрии: пересечение высот треугольника ABC
Задача
Даны точки A(5; - 1), B(4; - 8), C(- 4; - 4). Найдите координаты точки пересечения высот треугольника ABC.
Решение
Найдём уравнение прямой BC по двум точкам:
$\displaystyle {\frac{y-(-8)}{-4-(-8)}}$ = $\displaystyle {\frac{x-4}{-4-4}}$, или y = - $\displaystyle {\textstyle\frac{1}{2}}$x - 6.
Тогда её угловой коэффициентk1= -${\frac{1}{2}}$. Еслиk2— угловой коэффициент
прямой, содержащей высотуAP, тоk1 . k2= - 1. Поэтому
k2 = - $\displaystyle {\frac{1}{k_{1}}}$ = 2.
Уравнение прямой, содержащей высотуAPтреугольникаABC, найдём по
точкеA(5; - 1) и угловому коэффициентуk2= 2:
y + 1 = 2(x - 5), или y = 2x - 11.
Найдём уравнение прямой AC по двум точкам:
$\displaystyle {\frac{y-(-1)}{-4-(-1)}}$ = $\displaystyle {\frac{x-5}{-4-5}}$, или y = $\displaystyle {\textstyle\frac{1}{3}}$x - $\displaystyle {\textstyle\frac{8}{3}}$.
Тогда её угловой коэффициентk3=${\frac{1}{3}}$. Еслиk4— угловой коэффициент
прямой, содержащей высотуBQ, тоk4 . k3= - 1. Поэтому
k4 = - $\displaystyle {\frac{1}{k_{3}}}$ = - 3.
Уравнение прямой, содержащей высотуBQтреугольникаABC, найдём по
точкеB(4; - 8) и угловому коэффициентуk4= - 3:
y + 8 = - 3(x - 4), или y = - 3x + 4.
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений,
задающих прямые AP и BQ:
$\displaystyle \left\{\vphantom{ \begin{array}{lll}
y=2x-11\\
y = -3x+4.\\
\end{array} }\right.$$\displaystyle \begin{array}{lll}
y=2x-11\\
y = -3x+4.\\
\end{array}$
Получим:x= 3,y= - 5.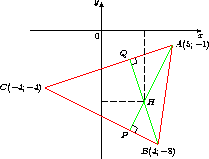
Ответ
(3; - 5).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет