Олимпиадная задача по планиметрии: уравнение касательной к окружности из точки A(0;7)
Задача
Составьте уравнение прямой, проходящей через точку A(0;7) и касающейся окружности (x - 15)2 + (y - 2)2 = 25.
Решение
Пусть k — угловой коэффициент искомой касательной. Тогда уравнение касательной имеет вид y - 7 = k(x - 0), или y = kx + 7. Данная задача сводится к нахождению всех таких чисел k, для которых система уравнений
$\displaystyle \left\{\vphantom{ \begin{array}{lll}
(x -15)^{2} + (y - 2)^{2} = 25\\
y = kx+7\\
\end{array} }\right.$$\displaystyle \begin{array}{lll}
(x -15)^{2} + (y - 2)^{2} = 25\\
y = kx+7\\
\end{array}$
имеет ровно одно решение.
Подставив y = kx + 7 в первое уравнение, после очевидных упрощений получим квадратное
уравнение
(k2 + 1)x2 + 10x(k - 3) + 225 = 0.
Это уравнение имеет единственное решение тогда и только тогда, когда его дискриминант равен 0,
т.е.
D = 102(k - 3)2 - 4 . 225(k2 + 1) = 100(- 8k2 - 6k) = 0.
Отсюда находим, чтоk= 0 илиk= -${\frac{3}{4}}$.
Следовательно, искомое уравнение имеет вид y = 7 или
y = - ${\frac{3}{4}}$x + 7.
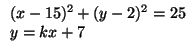
Ответ
y = 7 или y = - ${\frac{3}{4}}$x + 7.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет