Олимпиадная задача: координаты точки пересечения медиан треугольника, 8-9 класс
Задача
Докажите, что координаты точки пересечения медиан треугольника есть средние арифметические соответствующих координат вершин треугольника.
Решение
Пусть A(x1, y1), B(x2, y2) и C(x3, y3) – вершины
треугольника, M(x0, y0) – точка пересечения его медиан. Первый способ. Известно, что для любой точки O верно равенство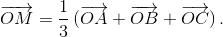 
.
Пусть O(0, 0) – начало координат. Тогда координаты векторов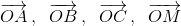 
есть координаты точек A, B, C и M соответственно. Следовательно, указанное выше векторное равенство равносильно двум числовым равенствам: x0 = ⅓ (x1 + x2 + x3), y0 = ⅓ (y1 + y2 + y3). Второй способ. Известно, что медианы треугольника делятся точкой пересечения в отношении 2 : 1, считая от вершины. Поэтому, если 
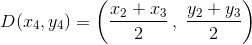(см. задачу 208531) – середина отрезка BC, то AM : MD = 2 : 1.
Поскольку точка M(x0, y0) делит отрезок с концами в точках A(x1, y1) и D(x4, y4) в отношении 2 : 1, считая от точки A, то по теореме о пропорциональных отрезках проекция точки M на ось OX делит проекцию отрезка AD на эту ось в том же отношении, то есть 
= 2. Отсюда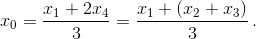 
Аналогично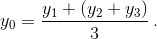 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь