Олимпиадная задача: доказательство общего уравнения прямой в декартовых координатах
Задача
Докажите, что любая прямая в декартовых координатах xOy имеет уравнение вида
ax + by + c = 0. где a, b, c — некоторые числа, причём хотя бы одно из чисел a, b отлично от нуля.
Решение
Пусть l — произвольная прямая на плоскости XOY. Рассмотрим две различные точки
A(x1;y1) и B(x2;y2), симметричные относительно прямой l. Поскольку прямая l — серединный перпендикуляр к отрезку AB, то произвольная точка M(x;y) этой прямой равноудалена от концов отрезка AB. Координаты этой точки удовлетворяют уравнению
(x - x1)2 + (y - y1)2 = (x - x2)2 + (y - y2)2.
Обратно, если координаты точкиMудовлетворяют этому уравнению, то она равноудалена
от точекAиB, а значит, лежит на прямойl.
После раскрытия скобок и приведения подобных полученное уравнение примет вид:
2(x2 - x1)x + 2(y2 - y1)y + (x12 + y12 - x22 - y22) = 0.
Обозначив2(x2-x1) =a,2(y2-y1) =bиx12+y12-x22-y22, получим уравнение
ax + by + c = 0.
Поскольку точкиAиBразличны, то крайней мере одно из чиселaиbотлично от нуля.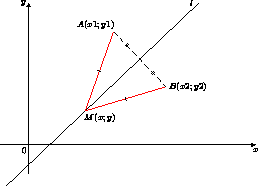
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет