Олимпиадная задача: Сколько моделей проволочных кубиков с шариками разных цветов?

Решение 1:Если кубик зафиксировать, то поместить 8 разных шариков в его вершины можно 8! способами. Но кубик можно поворачивать: каждую из шести его граней можно сделать нижней и поставить на нее четырьмя способами. Поэтому каждому кубику соответствуют  6·4 = 24  "раскраски", и общее число моделей равно  8! : 24 = 8·7·6·5 = 1680.

Решение 2:Сначала "наклеим" белый шарик. Повернём кубик так, чтобы белый шарик оказался в левом нижнем переднем углу. Теперь выберем 3 шарика для соседних вершин (это можно сделать 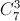    способами). "Наклеим" один из них и повернем кубик так, чтобы это шарик оказался в правом нижнем переднем углу (а белый остался на месте). Теперь есть два способа наклеить отбранные два шарика в оставшиеся две вершины, соседние с белой. И в каждом из них еще 4! способов "наклеить" оставшиеся четыре шарика на оставшиеся четыре вершины. Всего  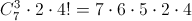   моделей.

1680 моделей.