Олимпиадная задача по планиметрии: биссектрисы и вписанный четырёхугольник
Задача
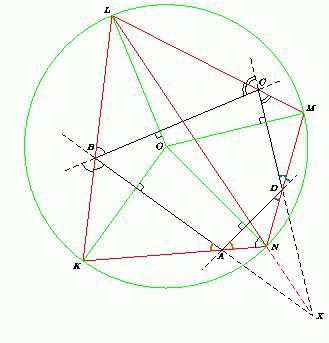
В выпуклом четырёхугольнике ABCD провели биссектрисы la, lb, lc и ld внешних углов при вершинах A, B, C и D соответственно. Точки пересечения прямых la и lb, lb и lc, lc и ld, ld и la обозначили через K, L, M и N. Известно, что три перпендикуляра, опущенных из точки K на AB, из L на BC, из M на CD пересекаются в одной точке. Докажите, что четырёхугольник ABCD – вписанный.
Решение
Обозначим через O точку пересечения перпендикуляров. опущенных из точки K на AB, из L на BC, из M на CD. Обозначим также ∠BAK = ∠DAN = α,
∠CBL = ∠ABK = β, ∠DCM = ∠BCL = γ, ∠ADN = ∠CDM = δ.
Тогда 2(α + β + γ + δ) = 360° как сумма внешних углов четырёхугольника ABCD. Из треугольников AKB и CMD находим, что
∠AKB + ∠CMD = (180° – α – β) + (180° – γ – δ) = 360° – (α + β + γ + δ) = 180°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь