Олимпиадная задача по планиметрии для 8–9 классов: отношение отрезков в параллелограмме
Задача
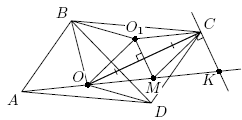
Дан параллелограмм ABCD с углом A, равным 60°. Точка O – центр описанной окружности треугольника ABD. Прямая AO пересекает биссектрису внешнего угла C в точке K. Найдите отношение AO : OK.
Решение
Угол при вершине A треугольника ABC – острый, поэтому вершина A и центр O описанной окружности этого треугольника лежат по одну сторону от прямой BD. ∠BOD = 2∠BAD = 120° = 180° – ∠BCD. Значит, четырёхугольник OBCD – вписанный. Поскольку вписанные углы BCO и DCO опираются на равные хорды OB и OD, то CO – биссектриса угла BCD, а так как CK – биссектриса смежного с ним угла, то ∠OCK = 90°.
Ответ
2 : 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет