Олимпиадная задача по планиметрии: доказательство перпендикулярности в треугольнике ABC (Сонкин М.)
Задача
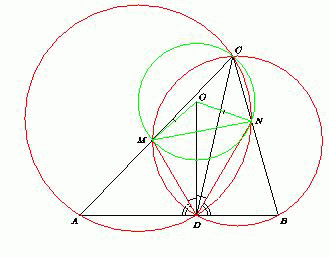
На стороне AB треугольника ABC выбрана точка D . Окружность, описанная около треугольника BCD , пересекает сторону AC в точке M , а окружность, описанная около треугольника ACD , пересекает сторону BC в точке N (точки M и N отличны от точки C ). Пусть O – центр описанной окружности треугольника CMN . Докажите, что прямая OD перпендикулярна стороне AB .
Решение
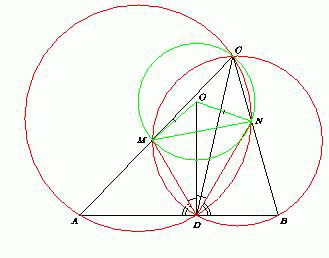
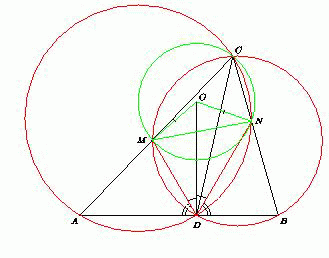
Рис. 1
 ADC
ADC 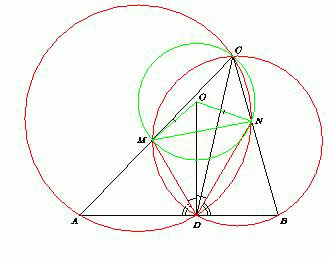 90o.
Обозначим
90o.
Обозначим ACB = γ.
ACB = γ.
Из условия задачи следует, что четырёхугольник ACND – вписанный,
причём точки N и D лежат по одну сторону от прямой AC ,
поэтому  ANC =
ANC =  ADC . В треугольнике ACN угол ANC не меньше90o , значит, угол ACN этого треугольника –
острый. Из этого следует, что в треугольнике MNC угол при вершине C – острый, т.е. γ < 90o . Поэтому вершина C и
центр O описанной окружности треугольника MNC лежат по одну
сторону от прямой MN . Поскольку MON – центральный угол этой
окружности, а MCN – вписанный, то
ADC . В треугольнике ACN угол ANC не меньше90o , значит, угол ACN этого треугольника –
острый. Из этого следует, что в треугольнике MNC угол при вершине C – острый, т.е. γ < 90o . Поэтому вершина C и
центр O описанной окружности треугольника MNC лежат по одну
сторону от прямой MN . Поскольку MON – центральный угол этой
окружности, а MCN – вписанный, то
 MON = 2
MON = 2 MCN = 2γ.
MCN = 2γ.
 ADM = 180o-
ADM = 180o- BDM =
BDM =  BCM = γ,
BCM = γ,
 BDN = 180o-
BDN = 180o- ADN =
ADN =  ACN = γ.
ACN = γ.
 MDN = 180o - (
MDN = 180o - ( ADM +
ADM +  BDN) = 180o-2γ,
BDN) = 180o-2γ,
 MDN +
MDN +  MON = (180o-2γ) + 2γ = 180o,
MON = (180o-2γ) + 2γ = 180o,
 ADO =
ADO =  ADM+
ADM+ ODM =
ODM =  BDN +
BDN +  ODN =
ODN =  BDO,
BDO,
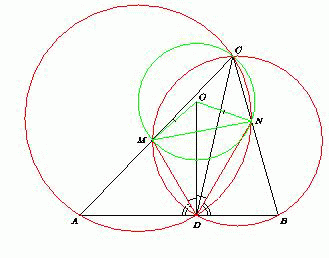 AB .
AB .
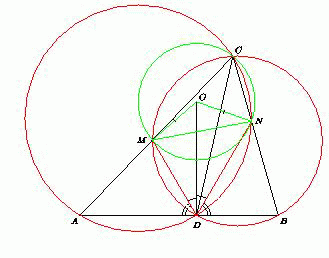
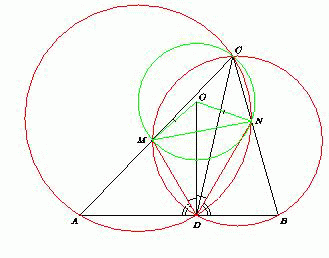
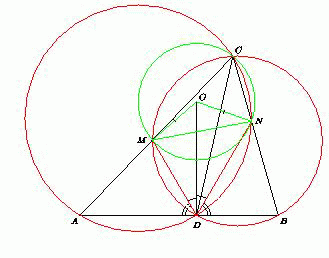
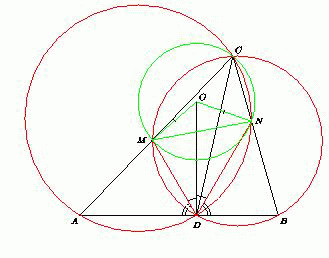
Рис. 2
 =
=  , но
, но
 =
=  (
( -
- )=
)=

 =
=  .
.
 =
=  и K=D , что и требовалось.
и K=D , что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь