Олимпиадная задача по планиметрии из окружностями и точками, 8–10 класс, Сонкин, Терешин
Задача
Окружности S1 и S2 пересекаются в точках M и N. Через точку A окружности S1 проведены прямые AM и AN, пересекающие окружность S2 в точках B и C, а через точку D окружности S2 – прямые DM и DN, пересекающие S1 в точках E и F, причём точки A, E, F лежат по одну сторону от прямой MN, а D, B, C – по другую (см. рис.). Докажите, что если AB = DE, то точки A, F, C и D лежат на одной окружности, положение центра которой не зависит от выбора точек A и D.
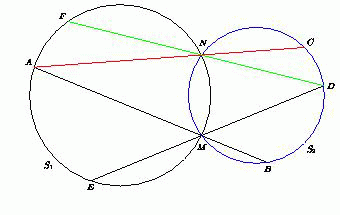
Решение
Лемма (теорема Н.И. Фусса). Пусть окружности S1 и S2 пересекаются в точках M и N. Через точку M проведена прямая, пересекающая S1 в точке E, S2 – в точке D, а через точку N – прямая, пересекающая S1 в точке A, S2 – в точке C. Тогда AE || CD.
Доказательство. Рассмотрим случай, изображённый на рис. слева, который соответствует условию решаемой задачи. В остальных случаях доказательство проводится аналогично.
Из вписанных четырёхугольников ANME и NCDM получаем, что ∠AEM = 180° – ∠ANM = ∠MNC = 180° – ∠MDC, то есть ∠AEM + ∠MDC = 180°. Следовательно,  AE || CD.
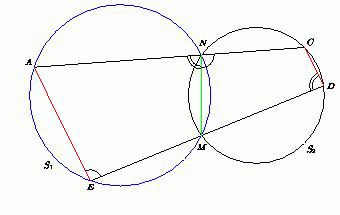
∠NBA = ∠NBM = ∠NDM = ∠NDE, а так как AB = DE, то треугольники ANB и END равны по стороне и двум прилежащим к ней углам.
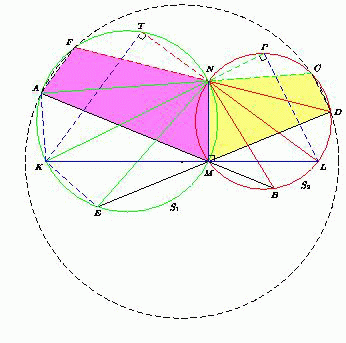
Пусть NK и NL – диаметры окружностей S1 и S2 соответственно. Тогда ∠KMN = ∠LMN = 90°, то есть точки K, M и L лежат на одной прямой, перпендикулярной MN.
Из равенства прямоугольных треугольников NAK и NEK по катету (NA = NE из равенства треугольников ANB и END) и общей гипотенузе NK следует равенство углов ANK и ENK. Аналогично, ∠DNL = ∠BNL . Значит, ∠AMK = ∠BML = ∠DML, ∠AMN = 90° – ∠AMK = 90° – ∠DML = ∠DMN.
Из вписанных четырёхугольников AFNM и DCNM получаем, что ∠AFD = ∠AFN = 180° – ∠AMN = 180° – ∠DMN = ∠DCN = ∠DCA.
Следовательно, точки A, F, C и D лежат на одной окружности. Докажем, что центр этой окружности – середина отрезка KL.
 : Пусть прямая KN вторично пересекает окружность S2 в точке P, а прямая LN вторично пересекает окружность S1 в точке T. Из равенства прямоугольных треугольников NAK и NEK следует, что точки A и E симметричны относительно прямой KP, поэтому KP ⊥ AE, а так как AE || CD (по лемме), то
KP ⊥ CD. Поскольку NP ⊥ PL (NL – диаметр окружности S2), то PL || CD. Значит, серединные перпендикуляры к параллельным хордам PL и CD совпадают. Аналогично докажем, что совпадают серединные перпендикуляры к отрезкам AF и KT.
Поскольку KL – общая гипотенуза прямоугольных треугольников KPL и KTL, а серединный перпендикуляр к катету проходит через середину гипотенузы, то серединные перпендикуляры к сторонам AF и CD вписанного четырёхугольника AFCD пересекаются в середине отрезка KL.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь