Олимпиадная задача по планиметрии для 9–11 классов от Сонкина М.: биссектрисы и симметрии в треугольнике
Задача
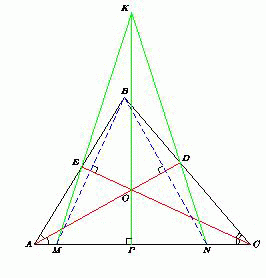
Биссектрисы AD и CE треугольника ABC пересекаются в точке O. Прямая, симметричная AB относительно CE, пересекает прямую, симметричную BC относительно AD, в точке K. Докажите, что KO ⊥ AC.
Решение
Пусть прямые KE и KD пересекают прямую AC в точках M и N соответственно. Поскольку CE – биссектриса, то при симметрии относительно прямой CE прямая AC переходит в прямую BC. По условию при этой симметрии прямая KM переходит в прямую AB, значит, точка пересечения M прямых AC и KM переходит при этой симметрии в точку пересечения прямых BC и AB, то есть в точку B. Поэтому треугольник CME переходит в треугольник CBE. Следовательно, ∠KMN = ∠EMC = ∠EBC = ∠ABC.
Аналогично ∠KNM = ∠ABC. Значит, треугольник KMN – равнобедренный, KM = MN. Кроме того, прямая CE – серединный перпендикуляр к отрезку BM, а прямая AD – серединный перпендикуляр к отрезку BN, значит, точка O их пересечения – центр описанной окружности треугольника MBN. Поэтому точка O, как и точка K лежит на серединном перпендикуляре l к отрезку MN.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь