Олимпиадная задача по планиметрии для 8–9 класса: доказательство с точками P и Q в треугольнике ABC
Задача
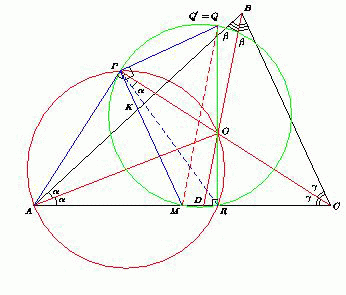
В треугольнике ABC (AB > BC) K и M – середины сторон AB и AC, O – точка пересечения биссектрис. Пусть P – точка пересечения прямых KM и CO, а точка Q такова, что QP ⊥ KM и QM || BO. Докажите, что QO ⊥ AC.
Решение
Пусть углы треугольника ABC равны 2α, 2β и 2γ соответственно. Опустим перпендикуляр OR на прямую AC. Пусть перпендикуляр к прямой KM, восставленный из точки P, пересекает прямую OR в точке Q'. Достаточно доказать, что MQ' || BO, так как это будет означать, что точки Q' и Q совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет