Олимпиадная задача по планиметрии для 7–9 класса от Агахановa Н. Х.: доказательство прямого угла
Задача
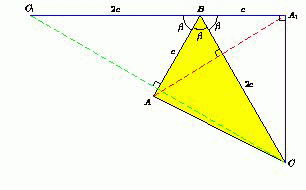
Дан треугольник ABC. Точка A1 симметрична вершине A относительно прямой BC, а точка C1 симметрична вершине C относительно прямой AB.
Докажите, что если точки A1, B и C1 лежат на одной прямой и C1B = 2A1B, то угол CA1B – прямой.
Решение
Обозначим ∠ABC = β, AB = c. По условию ∠A1BC = ∠C1BA = ∠B = β, BA1 = BA = c, BC1 = BC, а так как BC1 = 2BA1, то BC = 2c. Точки A1, B и C1 лежат на одной прямой, поэтому 3β = ∠A1BC + ∠ CBA + ∠ABC1 = 180°. Отсюда β = 60°. В треугольнике BA1C A1B = c, BC = 2c и ∠CBA1 = 60°. Следовательно, этот треугольник – прямоугольный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет