Олимпиадная задача по планиметрии для 7-9 классов: параллельность прямых в четырёхугольнике
Задача
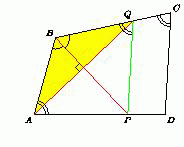
В четырёхугольнике ABCD углы A и C равны. Биссектриса угла B пересекает прямую AD в точке P. Перпендикуляр к BP, проходящий через точку A, пересекает прямую BC в точке Q. Докажите, что прямые PQ и CD параллельны.
Решение
Биссектриса угла AB является его осью симетрии. Поэтому точки A и Q симметричны относительно этой прямой и ∠BCD = ∠BAD = ∠BAP = ∠BQP. Следовательно, PQ || CD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет