Олимпиадная задача по планиметрии: общая точка окружностей в параллелограмме
Задача
Дан параллелограмм ABCD (AB < BC). Докажите, что описанные окружности треугольников APQ для всевозможных точек P и Q, выбранных на сторонах BC и CD соответственно так, что CP = CQ, имеют общую точку, отличную от A.
Решение
Центр окружности, описанной около каждого из треугольников APQ, лежит на серединном перпендикуляре l к отрезку PQ. Поскольку все треугольники PCQ – равнобедренные (CP = CQ), то l – биссектриса угла PCQ, то есть угла C. Окружность симметрична относительно каждого своего диаметра, поэтому точка A', симметричная точке A относительно прямой l, лежит на описанной окружности каждого из треугольников APQ. Итак, все указанные окружности проходят через точку A'. 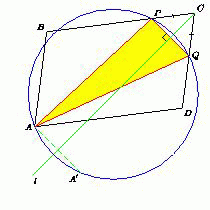
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь