Докажите, что четырёхугольник — параллелограмм: олимпиадная задача по планиметрии, 8-9 класс
Задача
Пусть ABCD – четырёхугольник с параллельными сторонами AD и BC; M и N – середины его сторон AB и CD соответственно. Прямая MN делит пополам отрезок, соединяющий центры окружностей, описанных около треугольников ABC и ADC. Докажите, что ABCD – параллелограмм.
Решение
Средняя линия трапеции (и параллелограмма) делит диагональ пополам, поэтому MN проходит через середину O диагонали AC.
Пусть O1 и O2 – центры описанных окружностей треугольников ABC и ADC соответственно.
Линия центров O1O2 перпендикулярна
общей хорде AC и проходит через её середину O. По условию MN проходит через середину O1O2. Следовательно, точка O и есть середина O1O2.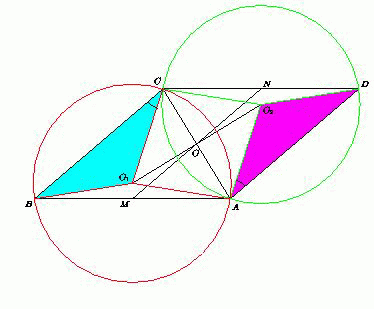 
Итак, отрезки AC и O1O2 перпендикулярны и делят друг друга пополам. Значит, AO1CO2 – ромб. Поэтому радиусы описанных окружностей
треугольников ABC и ADC равны.
Поскольку BC || AD и CO1 || AO2, то ∠BCO1 = ∠DAO2, и равнобедренные треугольники BCO1 и DAO2 равны. Поэтому BC = AD. Следовательно, ABCD – параллелограмм.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь