Олимпиадная задача по планиметрии: Углы в выпуклом четырехугольнике для 8-9 классов

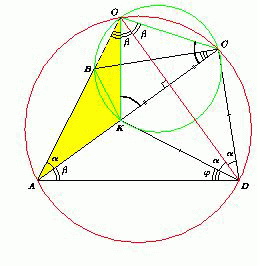
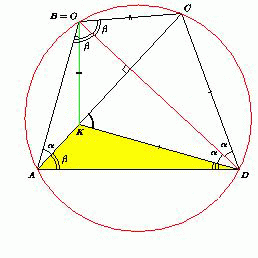
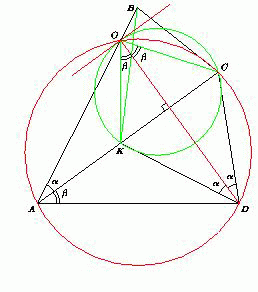
  Проведём биссектрису угла KDC до пересечения с прямой AB в точке O. Обозначим  ∠BAC = α,  ∠DAC = β,  ∠ADK = φ.  Возможны три случая.

  1) Точка O лежит на продолжении стороны AB за точку B. Поскольку  ∠ODC = ∠OAC = α,  то точки A, O, C и D лежат на одной окружности (рис. слева), поэтому  ∠DOC = ∠DAC = β,  ∠ACO = ADO = α + φ.

  Поскольку DO – биссектриса угла KDC и  KD = DC,  то DO – серединный перпендикуляр к отрезку KC. Значит,  ∠KOD = ∠DOC = β,

∠OKC = ∠OCK = ∠ACO = α + φ.

  Из точек B и O, лежащих по одну сторону от прямой KC, отрезок KC виден под углом 2β, значит, четырёхугольник KBOC – вписанный. Следовательно,  ∠BCA = ∠KOA = ∠OKC – ∠OAC = φ,  то есть  ∠BCA = ∠KDA.

  2) ТочкаOсовпадает сB. Поскольку  KB = BC  (рис. в центре), то  ∠CKD = 90° – α,  ∠KDA= ∠CKD– ∠CAD= 90° – α – β,  ∠OKC= 90° – β, ∠ABK= ∠OKC– ∠BAC= 90° – β – α,  то есть  ∠KDA= ∠KBA.   3) ТочкаOлежит на сторонеAB. Покажем, что этот случай невозможен. Предположим противное (рис. справа). Как и раньше,  ∠OAC= ∠ODC= α.  Поэтому четырёхугольникAOCD– вписанный, значит,  ∠COD= ∠CAD= β,  ∠KOC= 2∠COD= 2β = ∠KBC.   Следовательно, четырёхугольникKOBC– вписанный. Но касательная к описанной окружности равнобедренного треугольникаKOC, проведённая в точкеO, параллельнаAC, а точкаBлежит выше неё. Поэтому точкаBне может лежать на той же окружности. Противоречие.

Ответ задачи отсутствует