Олимпиадная задача по планиметрии: докажите, что BK = 2DC в треугольнике ABC
Задача
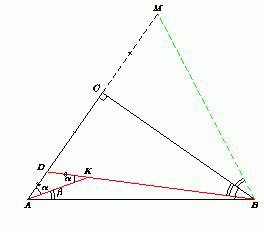
В треугольнике ABC угол C – прямой. На стороне AC нашлась такая точка D, а на отрезке BD – такая точка K, что ∠B = ∠KAD = ∠AKD.
Докажите, что BK = 2DC.
Решение
Пусть ∠B = ∠KAD = ∠AKD= α, ∠BAK = β.
На продолжении отрезка DC за точку C отложим отрезок CM = DC. Тогда высота BC треугольника DBM является его медианой, поэтому треугольник DBM – равнобедренный с основанием DM.
∠ABK = ∠AKD – BAK = α – β. Поэтому ∠CBM = ∠CBD = ∠B – ∠ABK = β, ∠ABM = α + β = ∠BAM.
Значит, треугольник ABM – равнобедренный с основанием AB, BM = AM = BD. Следовательно, BK = BD – DK = AM – AD = DM = 2DC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет