Олимпиадная задача: Доказательство пересечения прямых в планиметрии, 9–11 класс
Задача
Каждая из окружностей S1, S2и S3касается внешним образом окружности S (в точках A1, B1и C1соответственно) и двух сторон треугольника ABC (см.рис.). Докажите, что прямые AA1, BB1и CC1пересекаются в одной точке.
Решение
При гомотетии HA1, переводящей окружность S1в окружность S , прямые AB и AC перейдут в параллельные им прямые, касающиеся окружности S . Точка пересечения A прямых AB и AC перейдёт в некоторую точку A2пересечения их образов. Значит, точки A , A1и A2лежат на одной прямой.
Аналогично, гомотетии HB1и HC1, переводящие S2и S3в S , переводят соответственно прямые AB , BC и AC , BC в касательные к окружности S ,
соответственно параллельные этим прямым. При этом возникает
треугольник A2B2C2, гомотетичный треугольнику ABC (стороны треугольника A2B2C2соответственно
параллельны сторонам треугольника ABC ). Значит, прямые AA2, BB2и CC2пересекаются в одной точке –
центре гомотетии, переводящей треугольник ABC в треугольник A2B2C2, а т.к. точки A1, B1и C1лежат
соответственно на прямых AA2, BB2и CC2, то
прямые AA1, BB1и CC1пересекаются
в этой же точке.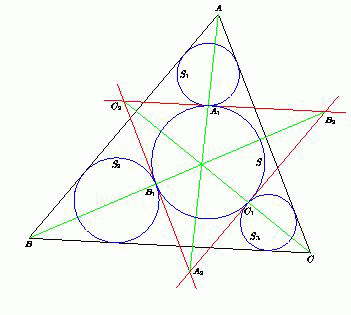
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь