Олимпиадная задача по планиметрии для 9-11 класса Терешина Д. А.: медианы и диаметр описанной окружности
Задача
Пусть a , b и c – стороны треугольника, ma , mb и mc – медианы, проведённые к этим сторонам, D – диаметр окружности, описанной около треугольника. Докажите, что
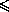 +
+ 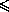 +
+
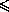
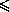 6D.
6D.
Решение
Пусть AB=c , AC=b , BC=a . Продолжим медианы AA1=ma , BB1=mb и CC1=mc треугольника ABC до пересечения с описанной окружностью треугольника в точках A2, B2и C2соответственно. Тогда
AA2 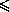 D, BB2
D, BB2 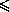 D, CC2
D, CC2 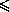 D,
D,
ma+A1A2 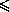 D, mb+B1B2
D, mb+B1B2 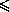 D,
mc+C1C2
D,
mc+C1C2 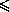 D.
D.
A1A2· AA1 = BA1· A1C 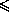 A1A2 =
A1A2 = 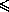 =
=
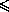 =
= 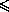 .
.
B1B2 =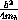 ,
C1C2 =
,
C1C2 =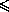 .
.
=(ma+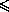 )+
(mb+
)+
(mb+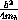 )+
(mc+
)+
(mc+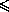 ) =
) =
= 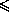 +
+
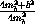 +
+
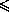
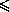 3D,
3D,
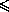 +
+ 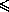 +
+
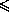
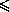 3D.
3D.
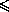 +
+ 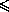 +
+
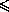
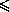 6D.
6D.
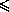
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет