Олимпиадная задача по планиметрии: равноудалённость точек P и Q в трапеции для 8-10 классов
Задача
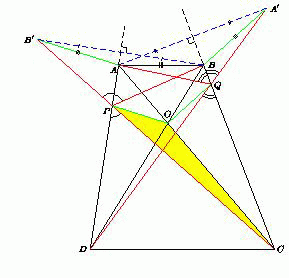
Трапеция ABCD такова, что на её боковых сторонах AD и BC существуют такие точки P и Q соответственно, что ∠APB = ∠CPD, ∠AQB = ∠CQD.
Докажите, что точки P и Q равноудалены от точки пересечения диагоналей трапеции.
Решение
Пусть точка B' симметрична вершине B относительно прямой AD. Тогда ∠APB' = ∠APB = ∠DPC. Значит, точки B', P и C лежат на одной прямой.
По теореме синусов AB : BP = sin∠APB : sin∠BAP = sin∠CPD : sin∠CDP = CD : PC, поэтому B'P : PC = BP : PC = AB : CD.
Пусть O – точка пересечения диагоналей трапеции ABCD. Из подобия треугольников AOB и COD следует, что AO : OC = AB : CD = B'P : PC. Поэтому AB' || OP. Значит, треугольники COP и CAB' подобны и OP = AB'·OC/CA = AB·CD/AB+CD.
Аналогично OQ = AB·CD/AB+CD = OP.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь