Олимпиадная задача по планиметрии для 7–9 классов — сравнение расстояний между городами A, B, C и D

Лемма. Дан отрезок XY. Геометрическое место точек Z, таких, что ZX > ZY, есть полуплоскость с границей l, содержащая точку Y, где l – серединный перпендикуляр к отрезку XY.Доказательство. Серединный перпендикуляр l к отрезку XY делит плоскость на две полуплоскости. Рассмотрим полуплоскость, содержащую точку Y (рис. 1). Докажем, что для любой точки Z этой полуплоскости ZX > ZY. Действительно, поскольку точки X и Z лежат в разных полуплоскостях с границей l, то отрезок ZX пересекает прямую l в некоторой точке T.

По свойству серединного перпендикуляра TX = TY, поэтому ZY < TY + TZ = TX + TZ = XZ.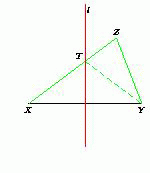Докажем теперь, что если ZY < ZX, то точки Y и Z лежат в одной полуплоскости с границей l.Точка Z не может лежать на прямой l, т.к. в этом случае ZY = ZX. Если же точки Y и Z лежат по разные стороны от прямой l, то точки Z и X лежат по одну сторону от этой прямой. В этом случае (см. первую часть доказательства) ZY > ZX, что противоречит условию.

Лемма доказана.Рассмотрим теперь нашу задачу. Проведём серединный перпендикуляр l к отрезку CD (рис. 2). Поскольку AC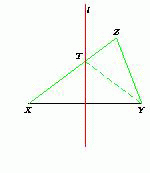 и BC, то по доказанной лемме точки A и B лежат в той полуплоскости с границей l, которая содержит точку C. Значит, любая точка M отрезка AB также лежит в этой полуплоскости. Следовательно, MC < MD.

Ответ задачи отсутствует