Олимпиадная задача по планиметрии для 8-9 класса: выпуклый четырёхугольник и точка O
Задача
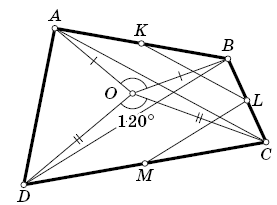
Дан выпуклый четырёхугольник ABCD и точка O внутри него. Известно, что ∠AOB = ∠COD = 120°, AO = OB и CO = OD. Пусть K, L и M – середины отрезков AB, BC и CD соответственно. Докажите, что
а) KL = LM;
б) треугольник KLM – правильный.
Решение
а) При повороте на 120° вокруг точки O отрезок AC переходит в BD, а значит, их длины равны (см. рис.). Отрезок KL является средней линией треугольника ABC, поэтому он параллелен отрезку AC, а его длина равна половине длины отрезка AC.
Аналогично отрезок LM параллелен отрезку BD, а его длина равна половине длины этого отрезка. Поэтому KL = LM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет