Олимпиадная задача по планиметрии для 8-9 класса: площадь треугольника через радиус описанной окружности
Задача
На сторонах AB , BC и AC треугольника ABC взяты точки C' , A' и B' соответственно. Докажите, что площадь треугольника A'B'C' равна
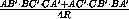 ,
,
Решение
Поскольку SΔ ABC=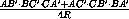 ,
достаточно доказать, что
,
достаточно доказать, что
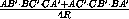 =
=
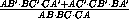 .
.
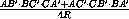 = x,
= x, 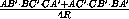 = y,
= y, 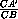 = z.
= z.
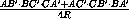 =
=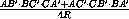 ·
· 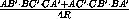 = x(1-y),
= x(1-y),
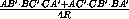 =
=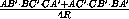 ·
· 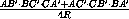 = y(1-z),
= y(1-z),
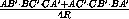 =
=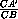 ·
· 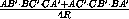 =z(1-x).
=z(1-x).
SΔ A'B'C' = (1- x(1-y) - y(1-z)- z(1-x))SΔ ABC=
=(xyz+(1-x)(1-y)(1-z))SΔ ABC=
=(AB'· BC'· CA' + AC'· CB'· BA')SΔ ABC.
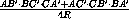
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет