Олимпиадная задача Произволова В. В. по планиметрии для 8-9 классов — равенство ломаных
Задача
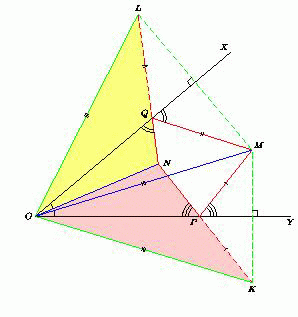
Внутри острого угла XOY взяты точки M и N, причём ∠XON = ∠YOM. На луче OX отмечена точка Q так, что ∠NQO = ∠MQX, а на луче OY – точка P так, что ∠NPO = ∠MPY. Докажите, что длины ломаных MPN и MQN равны.
Решение
Пусть точки L и K симметричны точке M относительно прямых OX и OY соответственно. Тогда точки K, P и N лежат на одной прямой, причём
NK = NP + PK = NP + PM.
Аналогично на одной прямой лежат точки N, Q и L, причём NL = NQ + QL = NQ + QM.
Треугольники KON и LON равны по двум сторонам (сторона ON – общая, OK = OM = OL) и углу между ними. Следовательно,
NP + PM = NK = NL = NQ + QM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет