Олимпиадная задача по планиметрии для 8–9 классов от Ковальджи А. К.: доказательство равенства площадей фигур в остроугольном треугольнике
Задача
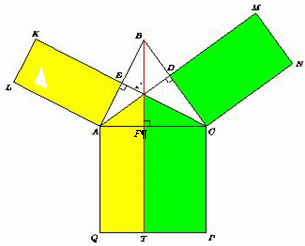
В остроугольном треугольнике ABC провели высоты AD и CE. Построили квадрат ACPQ и прямоугольники CDMN и AEKL, у которых AL = AB и
CN = CB. Докажите, что площадь квадрата ACPQ равна сумме площадей прямоугольников AEKL и CDMN.
Решение
Проведём третью высоту BF и продолжим её до пересечения с отрезком PQ в точке T. Прямоугольные треугольники ABF и ACE подобны, поэтому
AE : AC = AF : AB ⇒ AE·AB = AF·AC ⇒ SAEKL = AE·AL = AE·AB = AF·AC = AF·AQ = SAFTQ.
Аналогично SCDMN = SCFTP. Следовательно, SACPQ = SAFTQ + SCFTP = SAEKL + SCDMN.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет