Олимпиадная задача по планиметрии для 8–9 классов от Шаповалова А. В.
Задача
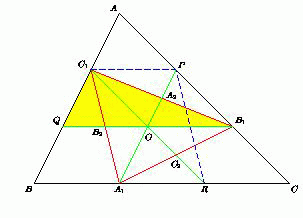
На сторонах BC, CA и AB треугольника ABC выбраны соответственно точки A1, B1 и C1, причём медианы A1A2, B1B2 и C1C2 треугольника A1B1C1 соответственно параллельны прямым AB, BC и CA. В каком отношении точки A1, B1 и C1 делят стороны треугольника ABC?
Решение
Пусть O – точка пересечения медиан треугольника A1B1C1. Продолжим медианы A1A2, B1B2 и C1C2 до пересечения с отрезками AC, AB и BC в точках P, Q и R соответственно. Поскольку отрезок OA2 проходит через середину A2 отрезка B1C1 и OA2 || C1Q, то OA2 – средняя линия треугольника B1C1Q. Поэтому O – середина B1Q. Аналогично O – середина отрезков A1P и C1R. Значит, A1C1PR – параллелограмм. Поэтому C1P = A1R и C1P || BC. Но тогда CRC1P и BA1PC1 – также параллелограммы (противоположные стороны этих четырёхугольников попарно параллельны). Значит, BA1 = C1P, CR = C1P. Следовательно, BA1 = A1R = CR и BA1 : B1A = 1 : 2. Аналогично CB1 : B1A = AC1 : C1B = 1 : 2.
Ответ
BA1 : A1C = CB1 : B1A = AC1 : C1B = 1 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь