Олимпиадная задача по планиметрии для 8-9 класса: касательные окружностей и центр вписанной
Задача
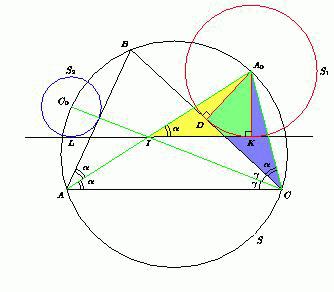
Треугольник ABC вписан в окружность S. Пусть A0 – середина дуги BC окружности S, не содержащей точку A, C0 – середина дуги окружности S, не содержащей точку C. Окружность S1 с центром A0 касается BC, окружность S2 с центром C0 касается AB. Докажите, что центр I вписанной в треугольник ABC окружности лежит на одной из общих внешних касательных к окружностям S1 и S2.
Решение
Из точки I проведём касательную IK к окружности S1 так, чтобы она пересекала меньшую дугу A0C. Аналогичным образом проведём касательную IL к окружности S2. Биссектриса AI угла BAC проходит через середину A0 дуги BC. Аналогично биссектриса CI проходит через C. Пусть ∠A = 2α, ∠ACB = 2γ. По теореме о внешнем угле треугольника ∠A0IC = α + γ.
С другой стороны, ∠A0CI = α + γ.
Значит, треугольник A0CI – равнобедренный, A0I = A0C. Окружность S1 касается BC в середине D стороны BC. Прямоугольные треугольники A0KI и A0DC равны по катету и гипотенузе, поэтому  ∠A0IK = ∠A0CD = α = ∠A0AC.
Следовательно, IK || AC. Аналогично, IL || AC. Таким образом, точки L, I, K лежат на одной прямой, параллельной AC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь