Олимпиадная задача: деление плоской выпуклой фигуры прямой (площадь и периметр)
Задача
Плоская выпуклая фигура ограничена отрезками AB и AD и дугой BD некоторой окружности (рис.1). Постройте какую-нибудь прямую, которая делит пополам: а) периметр этой фигуры; б) её площадь.
Решение
а) Достаточно провести прямую через середину дуги и середину ломаной BAD .
б) Пусть A – вершина угла BAD , B и D – концы дуги, C – её середина. Сегменты, опирающиеся на хорды BC и CD равны. Поэтому достаточно провести через точку C прямую, которая делит пополам площадь четырёхугольника ABCD .
Проведём через середину M диагонали BD прямую l , параллельную AC . Пусть она пересекает сторону AB в точке E (случай пересечения прямой l с со стороной AD рассматривается аналогично).
Точки B и D равноудалены от прямой l . Обозначим череза– их расстояния до прямой l , а через b – расстояние между параллельными прямыми AC и l . Тогда
SADCE = SΔ ACD + SΔ ACE =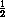 
AC(a-b) + 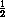AC· b=
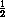AC· a,
SΔ BCE = SΔ ACB - SΔ ACE =
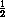AC(a+b) - 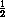AC· b =
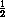AC· a = SADCE,
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь