Олимпиадная задача по планиметрии: пересечение прямых в треугольнике (9–11 класс)

  Пусть A₁, B₁ и C₁ – точки касания вписанной окружности со сторонами соответственно BC, AC и AB треугольника ABC. Через точку A₁ проведём прямую a₁, параллельную биссектрисе угла A. Поскольку треугольник B₁AC₁ равнобедренный, то биссектриса его угла при вершине A перпендикулярна основанию B₁C₁, значит, и прямая a₁ перпендикулярна B₁C₁. Поэтому высота треугольника A₁B₁C₁ лежит на прямой a₁.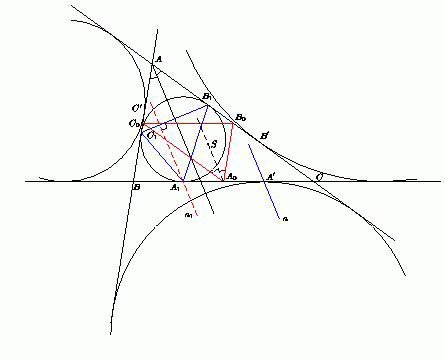   Пусть A₀, B₀ и C₀ – середины сторон BC, AC и AB соответственно. Поскольку при гомотетии с центром в точке пересечения медиан и коэффициентом –½ треугольник ABC переходит в треугольник A₀B₀C₀, то биссектрисы углов A и B₀A₀C₀ параллельны.

  Пусть S – точка пересечения биссектрис треугольника A₀B₀C₀. При симметрии относительно точки S прямая a₁ перейдёт в прямую a (прямые a₁, a и A₀S параллельны, а точки A₁ и A' прямых a₁ и a равноудалены от точки A₀ прямой A₀S – см. задачу 155404). Аналогично для прямых b₁ и b, c₁ и c.

  Таким образом, при этой симметрии каждая из высот треугольника A₁B₁C₁ перейдёт в соответствующую ей прямую a, b и c. Следовательно, эти прямые пересекутся в точке, симметричной ортоцентру треугольника A₁B₁C₁ относительно точки S.

Ответ задачи отсутствует