Олимпиадная задача по математике: треугольники и ортоцентры, 8-9 класс

Задача

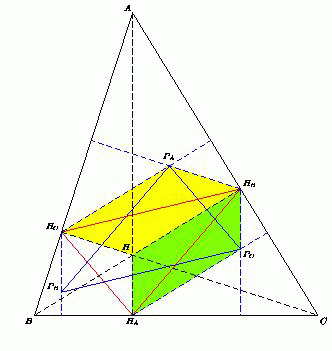
В остроугольном треугольнике ABC проведены высоты AH_A, BH_B и CH_C.

Докажите, что треугольник с вершинами в ортоцентрах треугольников AH_BH_C, BH_AH_C и CH_AH_B равен треугольнику H_AH_BH_C.

Решение

Пусть P_A, P_B, P_C и H – ортоцентры треугольников AH_BH_C, BH_AH_C, CH_AH_B и ABC соответственно. Поскольку H_BP_C || HH_A и H_AP_C || HH_B, то четырёхугольник H_AP_CH_BH – параллелограмм. Аналогично H_CP_AH_BH – параллелограмм. Значит, H_AP_C = HH_B = H_CP_A, H_AP_C || HH_B || H_CP_A. Поэтому и H_AP_CP_AH_C – параллелограмм. Следовательно, P_AP_C = H_AH_C. Аналогично P_BP_C = H_BH_C и P_AP_B = H_AH_B, и треугольники P_AP_BP_C и H_AH_BH_C равны по трём сторонам.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: равенство треугольников с ортоцентрами (8-9 класс)

Задача

Решение

Ответ

Подтверждение удаления