Олимпиадная задача по планиметрии для 8-9 классов от Емельянова Л. А.
Задача
В равнобедренном треугольнике ABC (AB = BC) средняя линия, параллельная стороне BC, пересекается со вписанной окружностью в точке F, не лежащей на основании AC. Докажите, что касательная к окружности в точке F пересекается с биссектрисой угла C на стороне AB.
Решение
Пусть указанная касательная пересекает стороны AB и BC в точках D и E соответственно, а прямую AC – в точке P. Точка касания M вписанной окружности со стороной AC – середина AC.
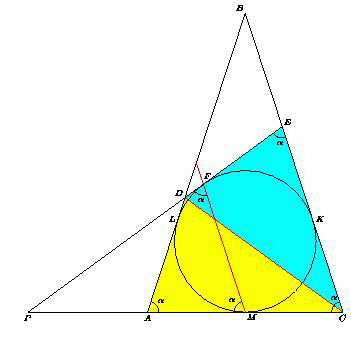 Обозначим ∠C = ∠CAB = α. Треугольник MPF – равнобедренный, поэтому ∠PEC =
∠PFM =∠PMF = ∠ACB = α.
Обозначим ∠C = ∠CAB = α. Треугольник MPF – равнобедренный, поэтому ∠PEC =
∠PFM =∠PMF = ∠ACB = α.
Пусть вписанная окружность треугольника ABC (она же вписанная окружность равнобедренного треугольника CPE) касается сторон BC и AB в точках K и L соответственно. Тогда FE = EK = KC = CM = AM = AL, поэтому AD = AL + LD = EF + DF = DE.
Значит, треугольники DAC и DEC равны по трём сторонам. Следовательно, CD – биссектриса угла C, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь