Олимпиадная задача: Центр описанной окружности и ортоцентр в треугольнике (планиметрия, 8-9 класс)
Задача
Радиус описанной окружности треугольника ABC равен радиусу окружности, касающейся стороны AB в точке C' и продолжений двух других сторон в точках A' и B' . Докажите, что центр описанной окружности треугольника ABC совпадает с ортоцентром (точкой пересечения высот) треугольника A'B'C' .
Решение
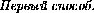 Докажем сначала следующее утверждение. Если противоположные стороны XY и ZT выпуклого четырёхугольника XYZT равны и при этом
Докажем сначала следующее утверждение. Если противоположные стороны XY и ZT выпуклого четырёхугольника XYZT равны и при этом  XYZ =
XYZ =
 YZT , то XYZT – равнобедренная трапеция или прямоугольник (рис.1).
Действительно, если XY || ZT , то XYZT – параллелограмм, а
т.к.
YZT , то XYZT – равнобедренная трапеция или прямоугольник (рис.1).
Действительно, если XY || ZT , то XYZT – параллелограмм, а
т.к.  XYZ = 180o -
XYZ = 180o -  YZT =
YZT =  YZT , то
YZT , то  XYZ =
XYZ =  YZT = 90o , т.е. XYZT – прямоугольник.
Пусть теперь прямые XY и ZT пересекаются в точке V . Будем считать, что
точка V лежит на продолжении стороны XY за точку Y . Тогда углы при
стороне YZ треугольника YVZ равны, поэтому он равнобедренный, а значит,
треугольник XVT также равнобедренный. Поскольку у равнобедренных
треугольников XVT и YVZ есть общий угол при вершине, то углы при их
основаниях также равны, т.е.
YZT = 90o , т.е. XYZT – прямоугольник.
Пусть теперь прямые XY и ZT пересекаются в точке V . Будем считать, что
точка V лежит на продолжении стороны XY за точку Y . Тогда углы при
стороне YZ треугольника YVZ равны, поэтому он равнобедренный, а значит,
треугольник XVT также равнобедренный. Поскольку у равнобедренных
треугольников XVT и YVZ есть общий угол при вершине, то углы при их
основаниях также равны, т.е.  VXT =
VXT =  VYZ , значит, YZ || XT . Следовательно, XYZT – равнобедренная трапеция.
Утверждение доказано.
VYZ , значит, YZ || XT . Следовательно, XYZT – равнобедренная трапеция.
Утверждение доказано.
Пусть вневписанная окружность (с центром O' ) данного треугольника ABC касается продолжений сторон CA и CB в точках B' и A' соответственно (рис.2). Обозначим углы данного треугольника ABC через α , β и γ соответственно. Тогда
 AOB = 2γ,
AOB = 2γ,  OAB =
OAB =  OBA = 90o-γ =
90o-(180o-α-β) = α + β -90o.
OBA = 90o-γ =
90o-(180o-α-β) = α + β -90o.
 O'AC' =
O'AC' = 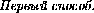
 B'AC' =
B'AC' = 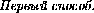 (180o-α)=
90o-
(180o-α)=
90o-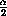 ,
,
 OAO' =
OAO' =  OAB +
OAB +  O'AC' = (α + β -90o)+
(90o-
O'AC' = (α + β -90o)+
(90o-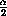 ) = β +
) = β + 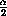 .
.
 A'O'B'= 180o -
A'O'B'= 180o -  A'CB' = 180o-γ, а
A'CB' = 180o-γ, а
 AO'B' = 90o-
AO'B' = 90o- O'AB' =
90o-
O'AB' =
90o- OAC' = 90o - (90o-
OAC' = 90o - (90o-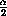 )=
)=
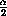 ,
,
 AO'A' =
AO'A' =  A'O'B' -
A'O'B' -  AO'B' = (180o-γ)-
AO'B' = (180o-γ)-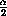 =
(α + β) -
=
(α + β) - 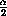 = β +
= β + 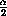 =
=  OAO'.
OAO'.
 B'C' то OA'
B'C' то OA' 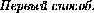 B'C' . Значит, высота треугольника A'B'C' , опущенная из вершины A' , лежит на прямой OA' . Аналогично докажем, что высота треугольника A'B'C' ,
опущенная из вершины B' , лежит на прямой OB' . Следовательно, O – ортоцентр
треугольника A'B'C' .
B'C' . Значит, высота треугольника A'B'C' , опущенная из вершины A' , лежит на прямой OA' . Аналогично докажем, что высота треугольника A'B'C' ,
опущенная из вершины B' , лежит на прямой OB' . Следовательно, O – ортоцентр
треугольника A'B'C' .
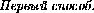 Пусть K – середина дуги BAC описанной окружности треугольника ABC (рис.3).
Тогда OK
Пусть K – середина дуги BAC описанной окружности треугольника ABC (рис.3).
Тогда OK 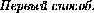 BC и O'A'
BC и O'A' 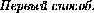 BC , поэтому OK || O'A' . Кроме того, OK =O'A' как радиусы равных окружностей, значит, четырёхугольник OKO'A' –
параллелограмм. Поэтому OA' || O'K .
BC , поэтому OK || O'A' . Кроме того, OK =O'A' как радиусы равных окружностей, значит, четырёхугольник OKO'A' –
параллелограмм. Поэтому OA' || O'K .
Если KL – диаметр описанной окружности треугольника ABC , то L – середина
дуги BC , не содержащей точки A , поэтому AL – биссектриса угла BAC , а т.к. AO' – биссектриса смежного с ним угла BAB' , то AO'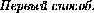 AL . С другой стороны,
поскольку точка A лежит на окружности с диаметром KL , то AK
AL . С другой стороны,
поскольку точка A лежит на окружности с диаметром KL , то AK 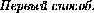 AL , значит,
точка A лежит на прямой O'K . Поскольку B'C'
AL , значит,
точка A лежит на прямой O'K . Поскольку B'C' 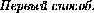 O'K и OA' || O'K ,
то B'C'
O'K и OA' || O'K ,
то B'C' 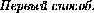 OA' . Это означает, что высота треугольника A'B'C' , опущенная из
вершины A' , лежит на прямой OA' . Аналогично докажем, что высота треугольника A'B'C' , опущенная из вершины B' , лежит на прямой OB' . Следовательно, O – ортоцентр треугольника A'B'C' .
OA' . Это означает, что высота треугольника A'B'C' , опущенная из
вершины A' , лежит на прямой OA' . Аналогично докажем, что высота треугольника A'B'C' , опущенная из вершины B' , лежит на прямой OB' . Следовательно, O – ортоцентр треугольника A'B'C' .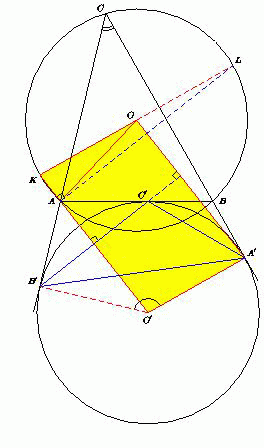
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь