Олимпиадная задача по планиметрии: неравенство для биссектрис и медиан, 8–9 класс, Канель-Белов

Докажем сначала следующее утверждение. Если точка $M$ лежит на стороне $YZ$ треугольника $XYZ$ и не совпадает с вершиной треугольника, то отрезок $XM$ меньше, чем наибольшая из сторон $XY$ и $XZ$.

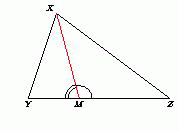Действительно, один из углов $XMY$ и $XMZ$ не меньше $90^\circ$. Пусть это угол $XMZ$. Тогда в треугольнике $XMZ$ против этого угла лежит наибольшая сторона, т.е. сторона $XZ$. Таким образом, отрезок $XM$ меньше одной из сторон $XY$ и $XZ$. Значит, он меньше наибольшей из этих сторон. Утверждение доказано. Пусть $a$, $b$ и $c$ – стороны соответственно $BC$, $AC$ и $AB$ треугольника $ABC$ ($a \le b \le c$); $l_a$, $l_b$, $l_c$ – биссектрисы треугольника, проведённые из соответствующих вершин; $m_a$, $m_b$, $m_c$ – соответствующие медианы; $I$ – точка пересечения биссектрис углов $A$ и $B$. 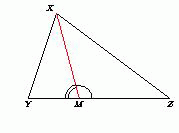Тогда по доказанному $m_a < c$ и $m_b < c$. Кроме того, для треугольника $AIB$ верно неравенство $AI+BI > AB = c$. Следовательно, $$\frac{l_a}{m_a} + \frac{l_b}{m_b} + \frac{l_c}{m_c} > \frac{l_a}{m_a} + \frac{l_b}{m_b} > \frac{l_a}{c}+\frac{l_b}{c} = \frac{l_a + l_b}{c} > \frac{AI+IB}{c} > \frac{c}{c}=1.$$

Ответ задачи отсутствует