Назад

Олимпиадная задача по планиметрии: параллельность отрезков в треугольнике ABC (Кожевников П. А.)

Задача 208103 • Сложность: 3 • 9-11 класс
Задача

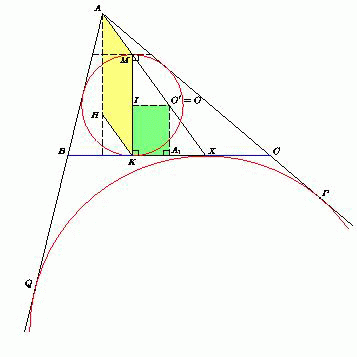
Дан треугольник ABC. В нём H – точка пересечения высот, I – центр вписанной окружности, O – центр описанной окружности, K – точка касания вписанной окружности со стороной BC. Известно, что отрезки  IO || BC.  Докажите, что отрезки  AO || HK.

Решение

  Пусть A1 – середина стороны BC. Как известно,  AH = 2OA1.  Поскольку OA1KI – прямоугольник, то  OA1 = IK.  Поэтому  AH = 2IK,  то есть отрезок AH равен диаметру вписанной окружности. Пусть M – точка этой окружности, диаметрально противоположная точке K. Поскольку  AH || KM  и  AH = AM,  то AHKM – параллелограмм, значит,  AM || HK.

  Рассмотрим гомотетию с центром в точке A, переводящую вписанную окружность треугольника ABC во вневписанную окружность этого треугольника, касающуюся стороны BC. При этой гомотетии касательная к вписанной окружности, проведённая через точку M, переходит в прямую BC, значит, точка M переходит в точку касания X вневписанной окружности со стороной BC. Как известно,  BK = CX  (см. задачу 155483).

  Следовательно,A1– середина отрезкаKX. Поскольку  A1O || KM  и  A1O= ½KM,  тоA1O– средняя линия треугольникаKMX. Таким образом, точкаOлежит на прямойAM, а  AM || HK.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет