Олимпиадная задача по планиметрии для 8-9 классов: прямая MI и треугольник ABC
Задача
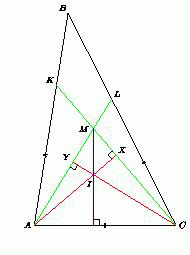
В треугольнике ABC сторона AC наименьшая. На сторонах AB и CB взяты точки K и L соответственно, причём KA = AC = CL. Пусть M – точка пересечения AL и KC, а I – центр вписанной в треугольник ABC окружности. Докажите, что прямая MI перпендикулярна прямой AC.
Решение
AI и CI – биссектрисы углов A и C. Пусть прямые AI и CK пересекаются в точке X, а прямые CI и AL – в точке Y. Поскольку треугольник KAC – равнобедренный (AC = AK по условию задачи), то его биссектриса AX является высотой. Значит, AX – высота треугольника AMC. Аналогично CY – высота этого треугольника. Итак, I – точка пересечения высот треугольника AMC. Следовательно, MI ⊥ AC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет