Олимпиадная задача по планиметрии: равенство треугольников в задаче для 7-9 классов
Задача
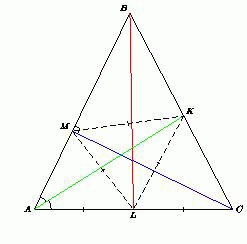
В треугольнике ABC проведены биссектриса AK, медиана BL и высота CM. Треугольник KLM – равносторонний.
Докажите, что треугольник ABC – равносторонний.
Решение
Заметим, что KL = ML = AL, то есть медиана KL треугольника AKC равна половине стороны AC. Поэтому этот треугольник – прямоугольный, то есть биссектриса AK треугольника ABC является его высотой. Следовательно, AB = AC, а K – середина BC. Значит, MK – медиана прямоугольного треугольника BMC, и BC = 2MK = 2KL = AC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет