Олимпиадная задача по планиметрии: площадь треугольника DCM в трапеции с вписанной окружностью. Класс 8-9, Толпыго А. К.
Задача
Дана трапеция ABCD, M – точка пересечения её диагоналей. Известно, что боковая сторона AB перпендикулярна основаниям AD и BC и что в трапецию можно вписать окружность. Найдите площадь треугольника DCM, если радиус этой окружности равен r.
Решение
Пусть O – центр вписанной окружности, K, L – точки ее касания со сторонами AD и BC. Напомним, что SDCM = SABM (см. зад. 156764). Способ 1. Пусть AD = a, BC = b – основания, h – высота трапеции.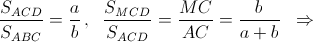 
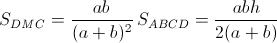(это верно в любой трапеции). CO и DO – биссектрисы углов C и D, поэтому ∠KDO + ∠LCO = 90°. Следовательно, прямоугольные треугольники KDO и LMO подобны, значит, KD·LC = r². Отсюда 
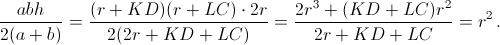Способ 2. В силу известного свойства описанного четырёхугольника (см. зад. 157022) отрезок KL (соединяющий противоположные точки касания) проходит через точку M. Точка O также лежит на этом отрезке. Поэтому SDCM = SABM = SABO = r².
Ответ
r².
Чтобы оставлять комментарии, войдите или зарегистрируйтесь