Олимпиадная задача по планиметрии: четырёхугольник из касательных, Кожевников
Задача
Отрезок AB пересекает две равные окружности и параллелен их линии центров, причём все точки пересечения прямой AB с окружностями лежат между A и B. Через точку A проводятся касательные к окружности, ближайшей к A, через точку B – касательные к окружности, ближайшей к B. Оказалось, что эти четыре касательные образуют четырёхугольник, содержащий внутри себя обе окружности. Докажите, что в этот четырёхугольник можно вписать окружность.
Решение
Решение 1: Пусть касательные образуют четырёхугольник ACBD. Обозначим через O1 и O2 центры окружностей.
Сдвинем правую часть картинки влево параллельно линии центров на расстояние O1O2. При этом окружности совпадут, а касательные, проведённые из точки B, перейдут в касательные, проведённые из точки B', лежащей на прямой AB (рис. слева).
Гомотетия с центром A и коэффициентом AD : AB' переводит точку B', в B, а прямую B'K – в параллельную ей прямую BD. Аналогично она переводит прямую B'L в BC. Поскольку прямые AD и AC переходят в себя, четырёхугольник AKB'L перейдёт в исходный четырёхугольник ADBC. Но четырёхугольник AKB'L описанный. Значит, и четырёхугольник ADBC описанный.
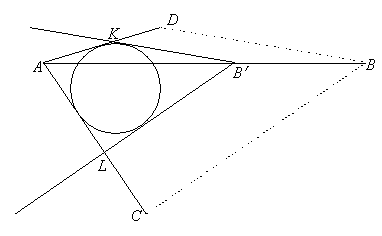
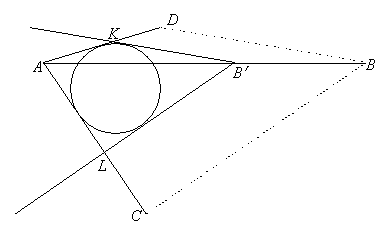
Решение 2: Обозначим через r радиус окружностей, через O – точку пересечения прямых AO1 и BO2 (рис. справа), а через d – расстояние от точек O1 и O2 до прямой AB. Прямая AO1 (BO2) – часть геометрического места точек, отношение расстояний от которых до прямых AC (BC) и AB равно r : d. Поэтому общая точка O прямых AO1 и BO2 равноудалена от прямых AC и BC. Кроме того, она равноудалена от сторон AC и AD (поскольку лежит на биссектрисе AO1 угла CAD) и от сторон BC и BD (по аналогичной причине). Значит, O равноудалена от всех сторон четырёхугольника ACBD, то есть является центром вписанной в него окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь