Олимпиадная задача по планиметрии: отношение OM к ON для отрезков в угле BOD (8-9 класс)
Задача
Отрезки AB и CD лежат на двух сторонах угла BOD (A лежит между O и B, C – между O и D). Через середины отрезков AD и BC проведена прямая, пересекающая стороны угла в точках M и N (M, A и B лежат на одной стороне угла; N, C и D – на другой). Докажите, что
OM : ON = AB : CD.
Решение
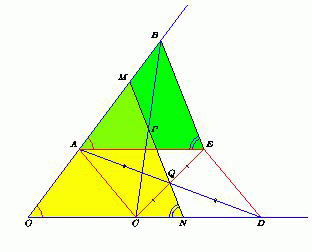
Пусть P – середина отрезка BC, Q – середина AD. На продолжении отрезка CQ за точку Q отложим отрезок QE, равный CQ. Тогда AEDC – параллелограмм, а точка Q – его центр. Поскольку PQ – средняя линия треугольника BCE, то PQ || BE, а значит, MN || BE. Кроме того, AE || ON, поэтому треугольники ABE и OMN подобны. Следовательно, OM : ON = AB : AE = AB : CD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет