Олимпиадная задача по планиметрии: докажите неравенство площади пятиугольника
Задача
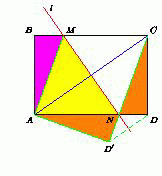
Прямоугольник ABCD с площадью 1 сложили по прямой так, что точка C совпала с A.
Докажите, что площадь получившегося пятиугольника меньше ¾.
Решение
Ясно, что ABCD – не квадрат (иначе при сложении получился бы треугольник). Пусть для определённости AB < BC. Так как точка C совпала с точкой A, то прямая сгиба l – серединный перпендикуляр к диагонали AC. Если M и N точки пересечения прямой l со сторонами BC и AD соответственно, то четырёхугольник AMCN – ромб, (его диагонали AC и MN перпендикулярны и делятся точкой пересечения пополам). Поэтому CM = AM > MB,
SCNM = ½ CM·AB < ½ BC·AB = ¼.
Пусть D' – точка, симметричная вершине D относительно прямой l. Тогда ABMND' – пятиугольник, полученный в результате сгиба, и
SABMND' = SABCD – SCMN = ¾.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь