Олимпиадная задача по планиметрии: равнобедренная трапеция и диагонали, 8-9 класс
Задача
В трапеции ABCD (AD – основание) диагональ AC равна сумме оснований, а угол между диагоналями равен 60°.
Докажите, что трапеция равнобедренная.
Решение
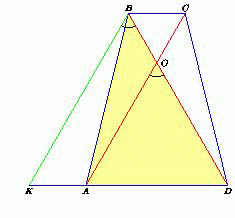
Пусть диагонали трапеции пересекаются в точке O. Построим параллелограмм ABCD. Тогда ∠KBD = ∠AOD, AK = BC и
KB = AC = BC + AD = AK + AD = KD. Значит, треугольник KBD – равнобедренный (KB = KD). Поскольку углы при основании равнобедренного треугольника – острые, то угол KBD не может быть равен 120°. Следовательно, он равен 60°, и треугольник KBD – равносторонний. Поэтому
BD = KB = AC, то есть диагонали трапеции равны между собой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет